How can we register three-dimensional points in space acquired from the same structure in different time-points? This is a problem I faced in my Ph.D. project where I was dealing with images of the same structure acquired at different time-points. For that project I was imaging dendritic spines, microscopic protrusions emanating from neurons, in alive mice (Figure 1).
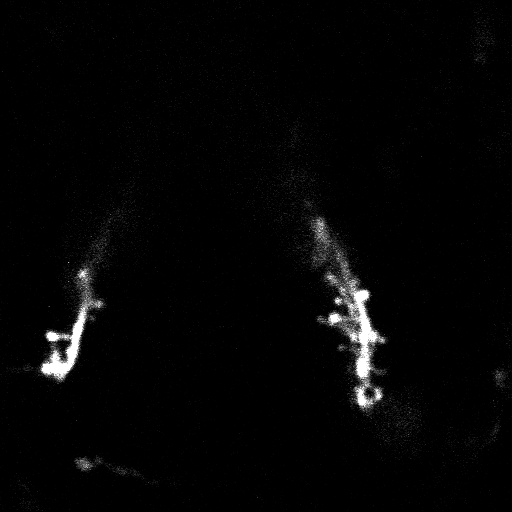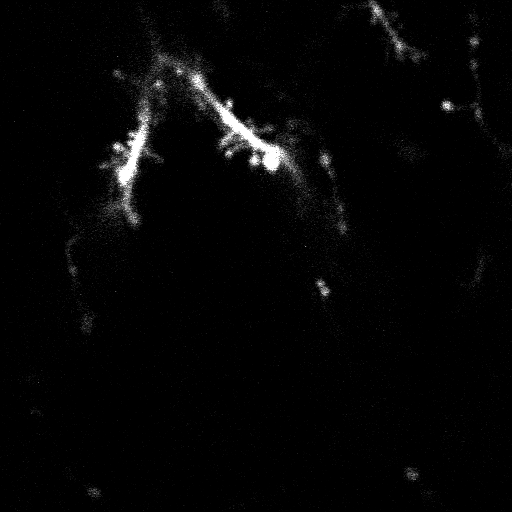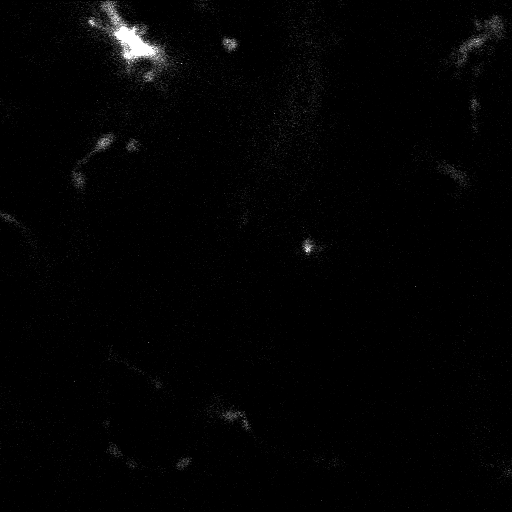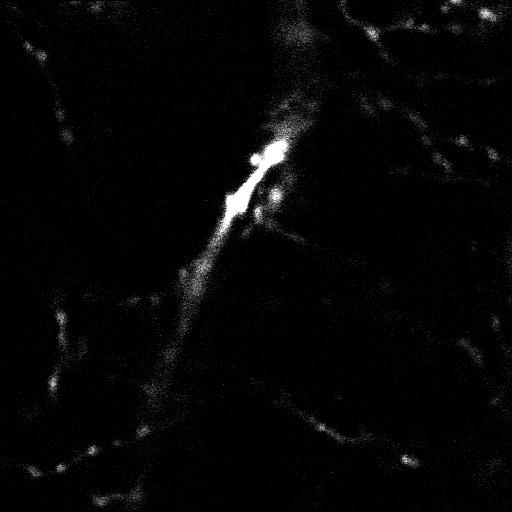
An image stack acquired from a spiny dendrite inside the brain of a live mouse
Every spine was assigned an ID and tracked over all available time-points, and we were interested in spine positions on the dendrite.
Even though I made every effort to acquire the images under similar conditions their alignment was never going to be perfect from one time-point to the next. To overcome the problems that such misalignments may cause when considering changes in distance to a fixed point over time, say a cortical column’s center or the surface of the brain, I had to perform some sort of image registration.
Two sources of information that can be useful when registering images are the intensity profiles of the image and the geometry of some of the image’s features. For example, we could choose to calculate some correlation metric based on the intensity values of the image as a whole. Alternatively, we could take into account the relative positions of some structures in the image in order to generate the geometrical transformation. In our case, since spine morphology can change a lot from session to session, especially since the animal received externally-generated stimulation, I chose to focus on the second approach.
A very simple method to register images based on feature coordinates is to apply a linear transformation, which assumes that no warping can occur between imaging sessions, i.e. the transformation is uniform across all structures considered. The possible transformations under this assumption are translation, rotation, scaling, and possibly reflection. The solution to finding the optimal linear transformation based on the sum of squared errors criterion is called procrustes analysis. Below I provide an example of procrustes analysis implemented in MATLAB for the dendrite shown in Figure 1.
(Please note: this post contains interactive visualizations through plot.ly which are best viewed in landscape mode on small screens.)
Implementation
First, let’s have a look at the data for this example:
data = readtable('data.csv'); % Load data
data = sortrows(data,'correlationID','ascend');
% Sort data based on correlation ID
disp(data(data.correlationID == 1, :))
% Select data for an example spine
session correlationID x0 x1 y0 y1 z
_______ _____________ ______ ______ ______ ______ __
1 1 7.1997 4.7421 33.728 33.421 13
2 1 8.0108 5.6118 32.435 32.26 13
3 1 8.1279 5.2061 32.497 32.387 13
4 1 9.4179 6.6599 34.94 35.295 17
5 1 11.554 8.9876 35.097 34.933 14
The above code loads the annotation data for the dendrite’s spines
and displays the data for a single spine.
The variable session refers to the imaging day,
correlationID to the spine identity,
x0 and y0 to the coordinates of the base of the spine,
x1 and y1 to the coordinates of the tip of the spine,
and z to the slice corresponding to the plane
in which the spine had the brightest fluorescence.
All coordinates are in micrometers.
Let’s then plot the annotations for all spines from the first session.
To do that I have defined a function, selectRows, that will simply
return all coordinates that match a logical index,
as I will be doing that a few times.
type('selectRows.m')
function [X, Y, Z] = selectRows(data, ind)
X = data.x0(ind);
Y = data.y0(ind);
Z = data.z(ind);
end
imatlab_export_fig('fig2plotly')
% Use the plotly graphics engine
% in a Jupyter notebook with the imatlab kernel
indSession1 = data.session == 1;
[X1, Y1, Z1] = selectRows(data, indSession1);
% Select coordinates from the first session for illustration
figure()
plot3(X1, Y1, Z1, 'ko', 'MarkerFaceColor', 'k')
We want to see what kind of displacements we are facing so I am going to add spines from the second session to the previous plot:
indSession2 = data.session == 2;
[X2, Y2, Z2] = selectRows(data, indSession2);
figure(); hold 'on';
plot3(X1, Y1, Z1, 'ko', 'MarkerFaceColor', 'k')
plot3(X2, Y2, Z2, 'ro', 'MarkerFaceColor', 'r')
legend('Session 1', 'Session 2')
We see that spines appear and disappear, and that part of the dendrite is shifted. Next, we will select those spines that are present in both the first and second sessions:
commonIDs = intersect(data.correlationID(indSession1), ...
data.correlationID(indSession2));
idInd = ismember(data.correlationID, commonIDs);
[sX1, sY1, sZ1] = selectRows(data, indSession1 & idInd);
[sX2, sY2, sZ2] = selectRows(data, indSession2 & idInd);
We are now ready to apply the procrustes analysis:
[d, XYZ, C] = procrustes([sX1, sY1, sZ1], [sX2, sY2, sZ2]);
The sum-of-squared-errors criterion is defined as:
$$ d = \sum _ {i=1 }^{n} \sum _ {j=1}^{p} (M _ {i,j} - N _ {i,j}) ^ 2 \enspace \text, \tag{1} $$
where $n$ the number of spines used for the registration,
$p$ the number of coordinates per spine $\{ x, y, z \}$, i.e. $p = 3$,
$M$ the coordinates of spines in the first session,
and $N$ the new set of coordinates for the second session after transformation. The function procrustes reports $d’$, stored in the above call in variable d, which is $d$ standarized by the sum of square errors of a centered version of $M$:
$$ d’ = \frac {d} {\sum \sum\limits _ {i = 1}^{n} {(M _ {i} - \overline{M})} ^ 2} \enspace \text, \tag{2} $$
where $\overline{M}$ the average $\{x, y, z \}$ coordinates across all spines of the first session.
In our example $d’$ was pretty low:
disp(d)
0.0145
which indicates that the registration was succesful.
The variable XYZ contains the transformed coordinates for the included spines of the second session.
We are not going to be using it since we are interested in applying the transformation to all spines of the second session, not just those that were also present in the first session.
The variable C contains the components for the tranformation:
disp(C)
T: [3×3 double]
b: 0.9974
c: [42×3 double]
T corresponds to the rotation and reflection component, b to the scale component, and c to the translation component. They are chosen so as to minimize $d’$ while satisfying the following equation:
$$ N = b*M’*T + c \tag{3}
$$
By simply applying this transformation to all spines of the second session we obtain the new coordinates:
N = C.b * [X2, Y2, Z2] * C.T + C.c(1,:);
Let’s now plot again the coordinates for spines from the first session and our new coordinates for spines from the second session, and see how we did:
figure(); hold on;
plot3(X1, Y1, Z1, 'ko', 'MarkerFaceColor', 'k')
plot3(X2, Y2, Z2, 'ro', 'MarkerFaceColor', 'r')
plot3(N(:,1), N(:,2), N(:,3), 'bo', 'MarkerFaceColor', 'b')
legend('Original Session 1', 'Original Session 2', 'Transformed Session 2')
You may want to use your mouse or finger to navigate through the image and click on the legend of the figure above to toggle viewing the corresponding data. We now simply need to write a function that runs all the above for all sessions.
type('applyProcrustes.m')
function [N] = applyProcrustes(data)
nSession = max(data.session);
sessVector = num2cell(2:nSession);
N = cellfun(@applyProcrustesSingleSession, ...
repmat({data}, length(sessVector), 1), sessVector', ...
'UniformOutput', 0);
function [N] = applyProcrustesSingleSession(data, iS)
indSession1 = data.session == 1;
indSession2 = data.session == iS;
[X2, Y2, Z2] = selectRows(data, indSession2);
commonIDs = intersect(data.correlationID(indSession1), ...
data.correlationID(indSession2));
idInd = ismember(data.correlationID, commonIDs);
[sX1, sY1, sZ1] = selectRows(data, indSession1 & idInd);
[sX2, sY2, sZ2] = selectRows(data, indSession2 & idInd);
[~, ~, C] = procrustes([sX1, sY1, sZ1], [sX2, sY2, sZ2]);
N = C.b * [X2, Y2, Z2] * C.T + C.c(1,:);
end
end
All we have done is to wrap our previous commands in a sub-function
which accepts the session variable in a generalized way,
and pass that function to cellfun that in turn applies it to data for all sessions.
The usage of cellfun over a conventional for-loop is advantageous in this case,
as it provides an order of magnitude gain in speed,
something that can make a difference if the function is run over many datasets.
One thing that we could have done differently is, instead of arbitrarily choosing one session (the first in our case) as the reference, we could take into account information from all sessions. For example, in generalized procrustes analysis the reference is chosen as an optimally determined “mean” shape. Such functionality is already implemented in the R package shapes.

Comments
No comments.
Submit comment