Welcome to Neurath’s boat, a blog about projects I am involved in, computational and analytical tools I find useful, and “thoughts in progress”.
The goals of this blog are for it to serve as:
- a personal archive, to avoid forgetting and to organize my thoughts
- a reference for other people who ask me stuff, following David Robinson’s advise: 1
When you’ve written the same code 3 times, write a function
— David Robinson (@drob) November 9, 2017
When you’ve given the same in-person advice 3 times, write a blog post
But who is Neurath and what about his boat? It may be useful to first provide some context in order to better appreciate the concept.
The foundations of knowledge
How do we know? This is the subject of a branch of philosophy called epistemology. A core question in epistemology is whether all of our knowledge comes from experience or if some knowledge can be acquired independently of experience, for example through reason. But is that possible? Empiricists like David Hume would argue that all knowledge proceeds from experience. But do we need knowledge from experience to know something that appears to be necessarily true, such as that $7 + 5 = 12$ ? If so, it remains possible that $7 + 5$ may not be equal to $12$ and that sounds counter-intuitive. Immanuel Kant came to argue that the foundations of knowledge are based on necessary truths that can be known as true without experience, such as propositions about space, time, and substance. But then all knowledge must be based on the metaphysical belief of their existence.
In the early twentieth century an influential philosophical movement called logical positivism attempted to provide a framework within which each proposition would either be necessarily true based on rules of formal logic or would be subject to verification based on experience, thus doing away with Kant’s metaphysical assumptions. But where would logic be founded on and how could the verification criterion itself be established?
Among the critics of logical positivism was Willard van Orman Quine who pointed out that the distinction between necessarily true propositions on the one hand and propositions that are verifiable through experience on the other was itself arbitrary; an article of metaphysical faith, the very thing that the positivists were trying to avoid. Instead, Quine proposed the doctrine of confirmation holism (Figure 1) according to which the whole body of empirical knowledge is tested with every new observation and no part of it is immune to revision; every recalcitrant observation, such that is not compatible with existing knowledge, affects the whole system of knowledge due to the interconnections between its parts.
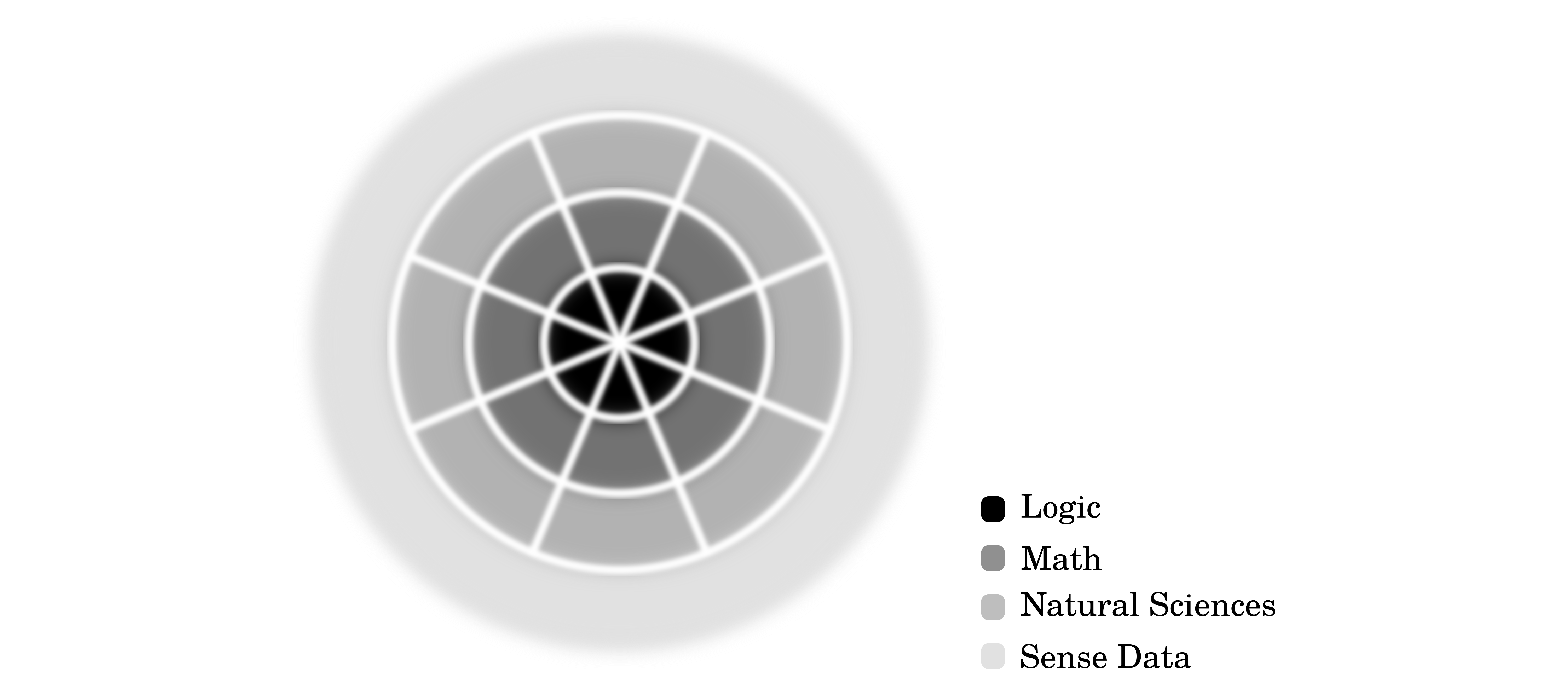
Schematic depiction of Quine’s confirmation holism.
While core components of the web of knowledge are more stable than those closer to the periphery, the system faces sense data as a whole and any of its components can be subject to revision. The borders between the sub-domains of science are fuzzy and incoming evidence can have an influence to all layers.
Even logic can be revised if that is required for the stability of the system as a whole. The sentiment behind the idea can be appreciated in a metaphor attributed to Otto Neurath (Jordi 2018) and popularized by Quine:
We are like sailors who have to rebuild their ship on the open sea, without ever being able to dismantle it in dry-dock and reconstruct it from its best components.
The consequence arising from Quine’s ideas is that we must use the tools of science to evaluate and understand how we come to knowledge rather than relying on metaphysical assumptions.
I have devoted my scientific career so far in studying how the brain acquires simple knowledge. Furthermore, I am convinced of the inter-dependence of philosophy and the scientific disciplines, and strive to bring together in my work different approaches to understanding and shaping the world.
This blog is a dedication to this effort.
References
Cat, Jordi, “Otto Neurath”, The Stanford Encyclopedia of Philosophy (Summer 2018 Edition)], Edward N. Zalta (ed.).
See also
Rysiew, Patrick, “Naturalism in Epistemology”, The Stanford Encyclopedia of Philosophy (Spring 2017 Edition), Edward N. Zalta (ed.).
Gödel’s incompleteness theorems. Wikipedia, The Free Encyclopedia (2018, March 29).
- My threshold is 2. ↥

Comments
No comments.
Submit comment