In this post, I will briefly cover the theory behind linear models that range from simple linear regression to generalized linear mixed models. In the companion post, I will go through the analysis of an example dataset with several different linear models to illustrate their practical applications. Once we understand the basic principles we will be able to construct and interpret more and more complex models with little extra effort.
Table of Contents
Linear Regression Models
Simple linear regression models are of the form:
$$ \hat{y} = \hat{\beta_1}x + \hat{\beta_0} + \hat{\epsilon} \label{eq:simple_linear_model} $$
where $\hat{y}$ is the response variable (also called the outcome or dependent variable), $x$ the predictor variable (also called stimulus or independent variable), $\hat{\beta_1}$ the coefficient estimate of the predictor variable, $\hat{\beta_0}$ the intercept estimate term (where all predictor variables are $0$), and $\hat{\epsilon}$ the error estimate. We describe the model as linear since it consists of a linear combination of the predictor variables. But the predictor variables themselves do not need to be linear. For example, the following is also considered a linear model:
$$ \hat{y} = \hat{\beta_1}x^2 + \hat{\beta_0} + \hat{\epsilon} \label{eq:linear_model_quadratic_term} $$
In the case that multiple predictors are included in the model we could write an equation of the form:
$$ \hat{y} = \hat{\beta_2}x_2 + \hat{\beta_1}x_1 + … + \hat{\beta_0} + \hat{\epsilon} \label{eq:verbose_linear_model} $$
However, this becomes cumbersome when we start including many variables in the model. Instead, we can use matrix notation to simplify long equations:
$$ \hat{y} = \hat{\beta}X + \hat{\epsilon} \label{eq:linear_model_matrix_notation} $$
where $\hat{y} = \begin{bmatrix} \hat{y_1} \\ \hat{y_2} \\ \vdots \\ \hat{y_n} \end{bmatrix}$, $X = \begin{bmatrix} 1 & x_{1,1} & \dots & x_{1,p} \\ 1 & x_{2,1} & \dots & x_{2,p} \\ 1 & \vdots & \ddots & \vdots \\ 1 & x_{n,1} & \dots & x_{n,p} \end{bmatrix}$, and $\hat{\beta} = \begin{bmatrix} \hat{\beta_0}, \enspace \hat{\beta_1}, \enspace \dots, \enspace \hat{\beta_p} \end{bmatrix}$ with $p$ the number of variables in the model including the intercept.
The column of $1$s in $X$ corresponds to the intercept term, and $x_{i,j}$ to different instantiations of a predictor variable. The matrix $X$ is often called the design matrix. The term $\hat{\beta}$ contains the estimated slopes for each corresponding variable of $X$. By re-arranging the terms of equation $\eqref{eq:linear_model_matrix_notation}$
$$ \hat{\epsilon} = y - \hat{\beta}X \label{eq:linear_model_error_term} $$
we can see that $\hat{\epsilon}$ is the residual error estimate, i.e. the part of $y$ that cannot be explained by $\hat{\beta}X$. An additionally simplifying assumption we often make when performing statistical inference with linear regression models is that the errors are independent and identically distributed, approximately following the normal distribution with mean $0$.
It is important to note that this assumption refers to the error term and not the response variable – it is perfectly possible that the response variable is not normally distributed and yet the residuals of a linear model are. To highlight this point consider the following example where $x$ is our predictor variable that can take either the value $-1$ or $1$, and we assume that $x$ is linearly related to $y$:
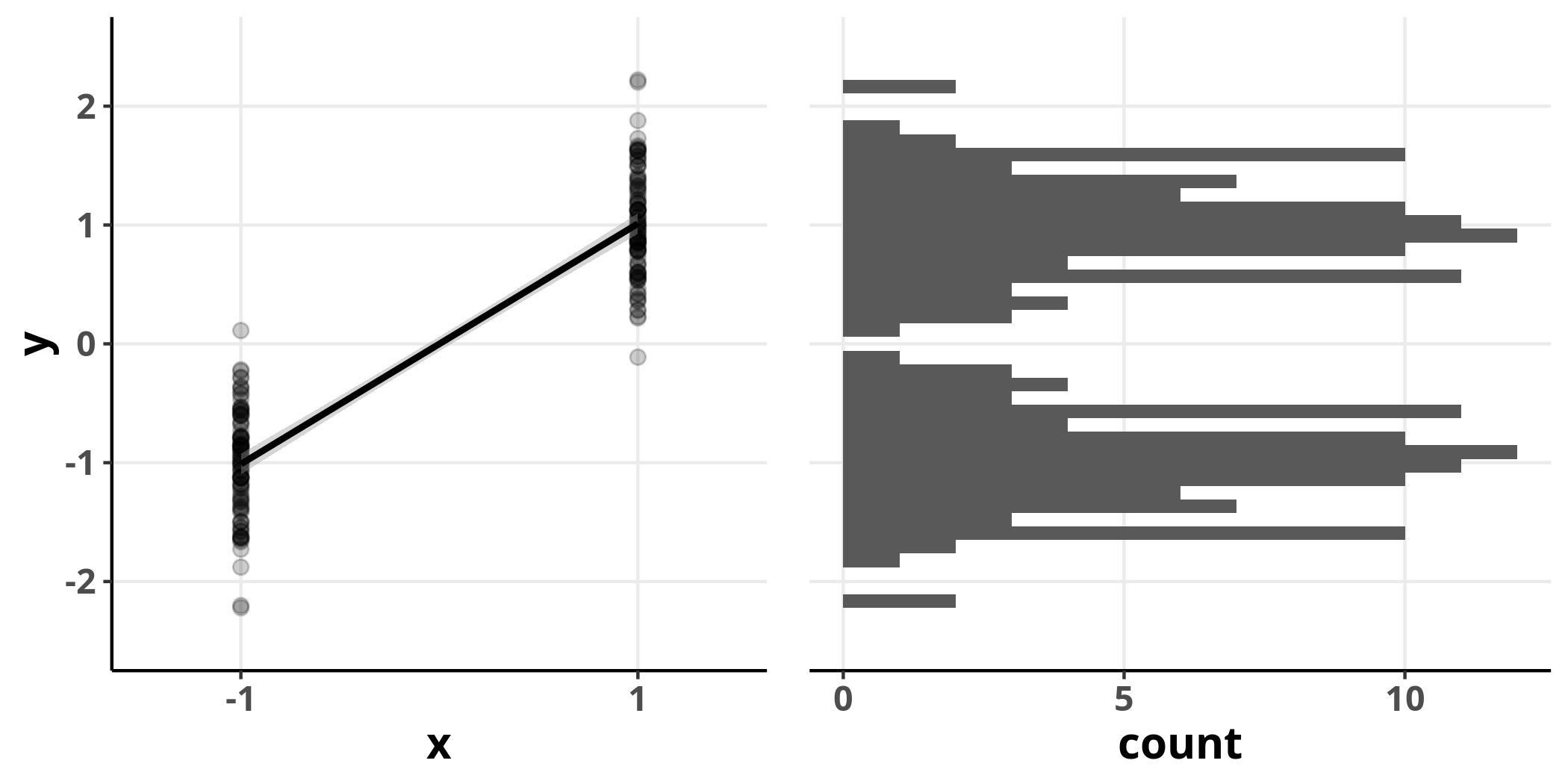
The distribution of $y$ is clearly bimodal and does not conform well to the normal distribution. However, we can still fit a linear model and evaluate its residuals.
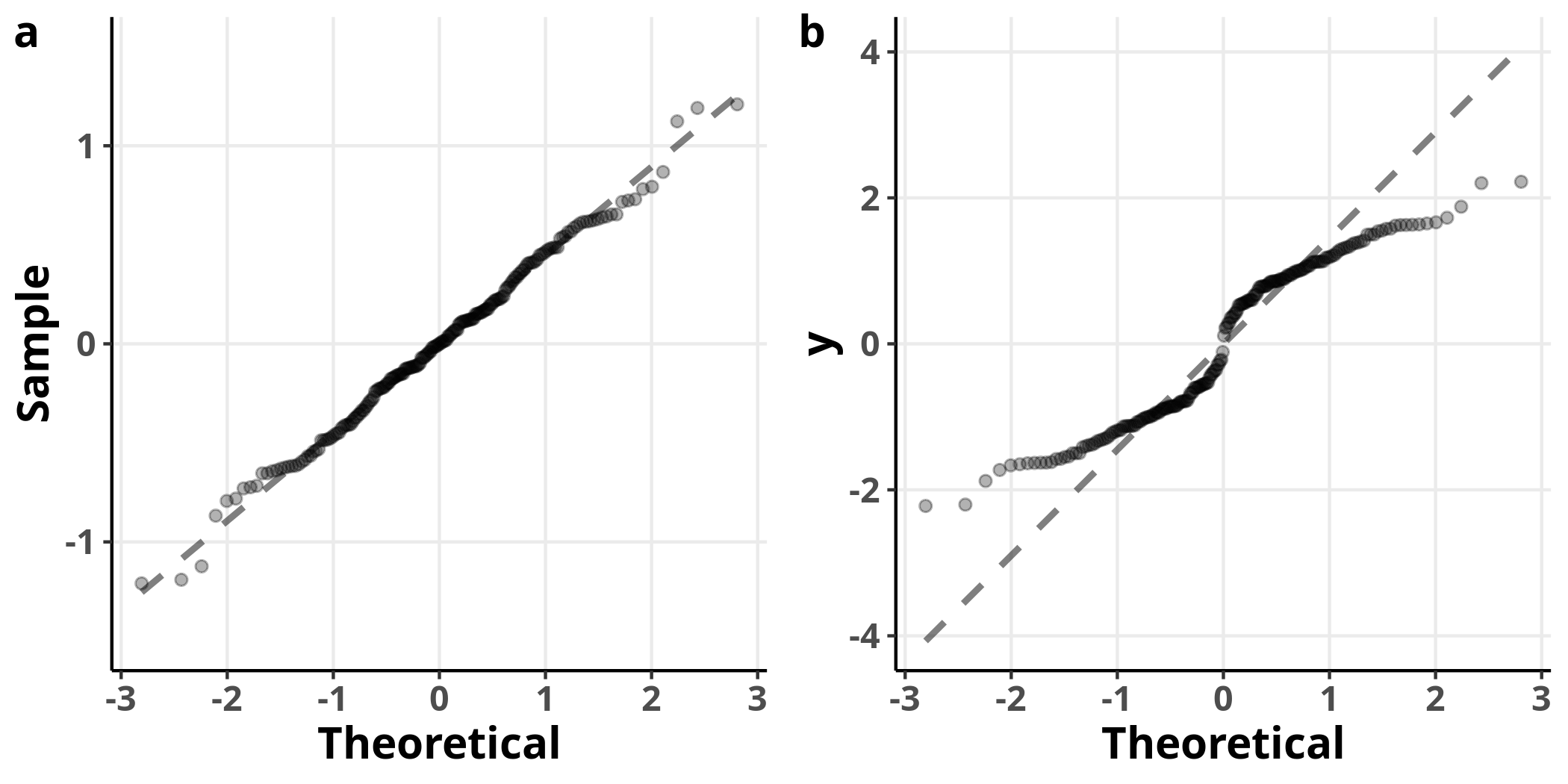
On the left, we see the Q-Q plot for the model’s residuals and on the right the Q-Q plot of the variable $y$, for reference. The model’s residuals are approximately normally distributed, while the response variable is not. It is, then, entirely appropriate to use a linear model in this case.
Semantics
It is often not apparent that the underlying model of an analysis of variance (ANOVA) is a special case of linear regression. The confusion may in part stem from the fact that the term ANOVA is often used to jointly refer to two distinct processes: the underlying linear model with categorical predictor variables and the F-test used to perform statistical inference on the linear model.
Linear regression models with more than one predictor variables are sometimes referred to as “General Linear Models” which should not be confused with “Generalized Linear Models” that we will discuss below.
Generalized Linear Models
In some cases, the assumptions of the linear model may not be valid. This is especially important when the response variable is expected to be better approximated with a distribution for which the variance depends on the mean or when the range of the response variable is restricted. For example, count outcomes can be in principle better described by the Poisson distribution which is defined for values equal to or greater than $0$ and its variance is equal to its mean. Generalized Linear Models (GLMs) address these issues. Under this class of models, the predictor estimates are still linear, but we can choose the response’s conditional distribution to be any one of the exponential family. Furthermore, the estimate of the response variable is expressed with a link function:
$$ g(\hat{y}) = \hat{\beta}X \label{eq:glm_link_function} $$
As an example, for the Poisson distribution the variance is $$ V(y) = \hat{y} \label{eq:poisson_var} $$ and the canonical link function is $$ g(\hat{y}) = log(\hat{y}) \label{eq:poisson_link} $$
When we choose the identity link function
$$ g(\hat{y}) = \hat{y} \label{eq:glm_identity} $$
and the normal distribution, the model becomes the simple linear model.
Linear Mixed-Effects Regression Models
Another extension of linear regression models is the framework of linear mixed-effects models (LMEs). LMEs address situations in which the response variable consists of non-independent measurements, such as when multiple measurements are obtained from the same unit (or subject) repeatedly. As such, LMEs are particularly useful for the analysis of longitudinal data and data that involve measurement replication. LMEs are also useful in cases where there is a hierarchical structure in the data, e.g. when we measure some variable from several classes of the same school –that is why they are also called hierarchical (or multilevel) models. The model is expressed as:
$$ \hat{y} = \hat{\beta}X + \hat{u}Z + \epsilon \label{eq:lme} $$
where $Z$ is the design matrix corresponding to the different units and $u$ the estimated coefficients for those units. Under this framework, the terms $\hat{\beta}X$ are referred to as fixed-effects and $\hat{u}Z$ as random-effects, hence the name mixed-effects for models that combine both of these classes of factors. The random-effects are assumed to approximately follow the normal distribution with mean $0$. Hence, only their variance (and covariance between random-effects terms, if more than one are included in the model) is estimated.
Generalized Linear Mixed-Effects Models
A natural extension of both GLMs and LMEs is to combine the two into a single framework, Generalized Mixed-Effects Models (GLMMs). GLMMs can accommodate data that are distributed according to any of the exponential family of distributions and are possibly acquired non-independently.
Estimation
In the case of linear regression models, the coefficient estimates can be obtained using the least-squares method, which has a closed-form solution. Briefly, the best approximation is found by minimizing the error estimate:
$$ S(\hat{\beta}) = {|| \hat{y} - \hat{\beta} X||}^2 \label{eq:regression_criterion} $$
and it can be shown that
$$ \hat{\beta} = (X^{T}X)^{-1}X^{T}y \label{eq:normal_equation} $$
Since the errors are assumed to be approximately normally distributed the least-squares estimate is also the maximum likelihood estimate (MLE). For LMEs and GLMMs, iterative algorithms are typically used to obtain the MLE.
Comments
No comments.
Submit comment